基于Python的机器学习实战：AadBoost

阿牛

目录:

1. Boosting方法的简介

2. AdaBoost算法

3.基于单层决策树构建弱分类器

4.完整的AdaBoost的算法实现

5.总结

1. Boosting方法的简介 返回目录
　　Boosting方法的基本思想：对于一个复杂的任务来说，将多个专家的判断进行适当的综合所得出的判断，要比其中任何一个专家单独的判断好. 实际上就是“三个臭皮匠顶个诸葛亮的道理。”（参考：李航 《统计学习方法》）
　　对于分类问题而言， 给定一个训练集，求比较粗糙的分类规则（弱分类器）要比求精确的分类规则（强分类器）容易得多。Boosting方法就是从弱学习算法出发，反复学习，得到一系列弱分类器（又称基本分类器），然后组合这些弱分类器，构成一个强分类器。
　　对于Boosting方法来说，需要回答两个问题：

• 每一轮如何改变训练数据的权值或者概率分布
  
• 如何将若分类器组合成一个强分类器
  

2. AdaBoost算法 返回目录
　　boosting 方法拥有多个版本，其中最流行的一个版本就是AdaBoost，即adaptive boosting.
　　对与上面提到的两个问题，AdaBoost的做法分别是：

• 对于第一个问题：提高那些被前一轮弱分类器错误分类的样本的权值，而降低那些被正确分类样本的权值.
  
• 对于第二个问题：采取加权多数表决的方法，具体就是，加大分类误差率较小的弱分类器的权值，使其在表决中起较大的作用，减小分类误差率大的弱分类器的权值，使其在表决中起较小的作用.
  

　　具体算法流程描述如下：

　　假定给定一个二分类的训练数据集
　　$T=\{(x_{1},y_{1}),(x_{2,}y_{2}),\cdots,(x_{N},y_{N})\}$
　　其中，每个样本点由实例与标记组成. 实例 $x_{i}\in X\subseteq R^{n}$ ，标记 $y_{i}\in Y$$\subseteq R^{n}$， $X$ 是实例空间，$Y$ 是标记集合.
　　输入：训练数据集 $T=\{(x_{1},y_{1}),(x_{2,}y_{2}),\cdots,(x_{N},y_{N})\}$，其中 $x_{i}\in X\subseteq R^{n}$， $y_{i}\in Y=\{-1,+1\}$；弱分类器；
　　输出：最终分类器 $G(x)$.
　　(1) 初始化训练数据的权值分布
　　$D_{1}=\{w_{11},\cdots,w_{1i},\cdots,w_{1N}\},w_{1N}=\frac{1}{N},i=1,2,\cdots,N$
　　初始化的时候让每个训练样本在基本分类器的学习中作用相同
　　(2) 对 $m=1,2,\cdots,M$
　　(a) 使用具有权值分布 $D_{m}$ 的训练数据学习，得到基本分类器
　　$G_{m}(x):X\longrightarrow\{-1,+1\}$
　　(b) 计算 $G_{m}(x)$ 在训练数据集上的分类误差
　　$e_{m}=P(G_{m}(x_{i})\neq y_{i})=\sum_{i=1}^{N}w_{mi}I(G_{m}(x_{i})\neq y_{i})$ (1)
　　(c) 计算 $G_{m}(x)$ 的系数
　　$\alpha_{m}=\frac{1}{2}\log\frac{1-e_{m}}{e_{m}}$ (2)
　　这里对数是自然对数. $\alpha_{m}$ 表示 $G_{m}(x)$ 在最终分类器中的重要性，由该式可知，当 $e_{m}\leq\frac{1}{2}$ 时，$\alpha_{m}\geq0$，并且 $\alpha_{m}$ 随着 $e_{m}$ 的减小而增大，所以误差率越小的基本分类器在最终分类器中的作用越大.
　　(d) 更新训练数据集的权值分布
　　$D_{m+1}=\{w_{m+1,1},\cdots,w_{m+1,i},\cdots,w_{m+1,N}\}$ (3)
　　$w_{m+1,i}=\frac{w_{mi}}{Z_{m}}\exp(-\alpha_{m}y_{i}G_{m}(x_{i})),i=1,2,\cdots,N$ (4)
　　这里 $Z_{m}$ 是归一化因子.
　　$Z_{m}=\sum_{i=1}^{N}w_{mi}\exp(-\alpha_{m}y_{i}G_{m}(x_{i}))$
　　它使 $D_{m+1}$ 成为一个概率分布. 式 (4) 还可以写成：
　　\[w_{m+1,i}=\left\{ \begin{array}{c}\frac{w_{mi}}{Z_{m}}e^{-\alpha_{m}},G_{m}(x_{i})=y_{i}\\\frac{w_{mi}}{Z_{m}}e^{\alpha_{m}},G_{m}(x_{i})\neq y_{i}\end{array}\right.\]
　　由此可知，被基本分类器 $G_{m}(x)$ 误分类样本的权值得以扩大，而被正确分类样本的权值却得以缩小，因此误分类样本在下一轮学习中起更大作用.
　　(3) 构建基本分类器的线性组合
　　$f(x)=\sum_{i=1}^{N}\alpha_{m}G_{m}(x)$
　　得到最终分类器
　　$G(x)=$sign$(f(x))=$sign$(\sum_{m=1}^{M}\alpha_{m}G_{m}(x))$
　　线性组合 $f(x)$ 实现 $M$ 个基本分类器的加权表决. $f(x)$ 的符号决定了实例 $x$ 的类别，$f(x)$ 的绝对值表示分类的确信度.

3.基于单层决策树构建弱分类器 返回目录
　　所谓单层决策树（decision stump, 也称决策树桩）就是基于简单的单个特征来做决策，由于这棵树只有一次分裂过程，因此实际上就是一个树桩。
　　首先通过一个简单的数据集来确保在算法实现上一切就绪.



def loadSimpData():
dataMat = np.matrix( [ [ 1., 2.1],
[ 2., 1.1],
[ 1.3, 1.],
[ 1., 1. ],
[ 2., 1. ] ] )
classLabels = [ 1.0, 1.0, -1.0, -1.0, 1.0 ]                           
return dataMat, classLabels
　　
　　下图给出了上面数据集的示意图
　　
　　
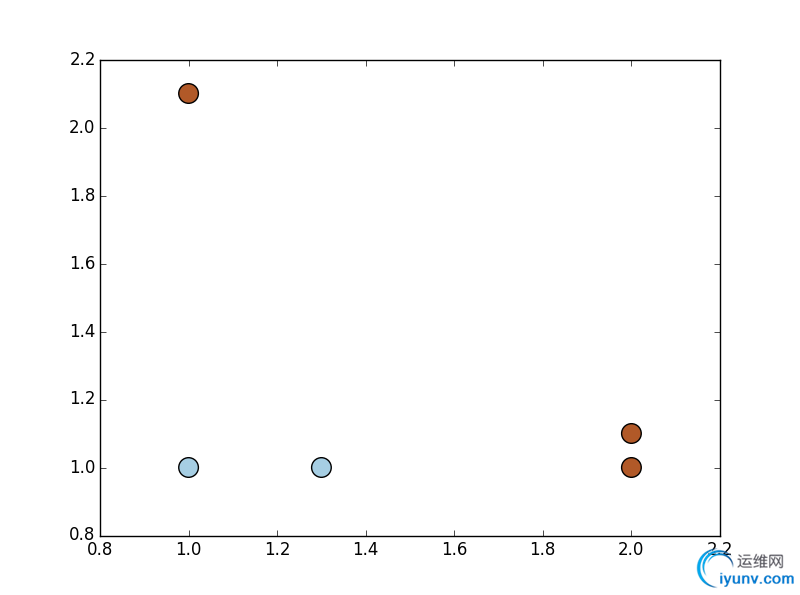
　　如果使用上面所述的单层决策树来对上面的样本点进行分类，即试着从某个坐标轴选择一个值（选择一条与坐标轴平行的直线）来将所有蓝色样本和褐色样本分开，这显然不可能。但是使用多棵单层决策树，就可以构建出一个能对该数据集完全正确的分类器.
　　首先给出单层决策树生成函数



def stumpClassify( dataMatrix, dimen, threshVal, threshIneq ):
'''
通过阈值比较对数据进行分类，所有在阈值一边的数据会分到类别-1，而在
另外一边的数据分到类别+1.   
'''
retArray = np.ones( ( np.shape( dataMatrix )[ 0 ], 1 ) )
if threshIneq == 'lt':
retArray[ dataMatrix[ :, dimen ] <= threshVal ] = -1.0
else:
retArray[ dataMatrix[ :, dimen ] > threshVal ] = -1.0
return retArray
def buildStump( dataArr, classLabels, D ):
'''
'''
dataMatrix = np.mat(dataArr)
labelMat = np.mat(classLabels).T
m,n = np.shape(dataMatrix)
numSteps = 10.0 #用于在特征的所有可能值上进行遍历
bestStump = {} #存储给定权重向量 D 时所得到的最佳单层决策树的信息
bestClassEst = np.mat( np.zeros( (m, 1) ) )
minError = np.inf
for i in range( n ):
# 对于每一维的特征
rangeMin = dataMatrix[:, i].min()
rangeMax = dataMatrix[:, i].max()
stepSize = ( rangeMax - rangeMin ) / numSteps
for j in range( -1, int( numSteps ) + 1 ):
# 对于每一个阈值
for inequal in [ 'lt', 'gt' ]:
threshVal = rangeMin + float( j ) * stepSize
predictedVals = stumpClassify( dataMatrix, i,
threshVal, inequal )
errArr = np.mat( np.ones( ( m, 1 ) ) )
errArr[ predictedVals == labelMat ] = 0
weightedError = D.T * errArr
#                print "split: dim %d, thresh %.2f, thresh inequal: \
#                    %s, the weighted error is %.3f" % \
#                    ( i, threshVal, inequal, weightedError )
if weightedError < minError:
minError =  weightedError
bestClassEst = predictedVals.copy()
bestStump[ 'dim' ] = i
bestStump[ 'thresh' ] = threshVal
bestStump[ 'ineq' ] = inequal
return bestStump, minError, bestClassEst
　　
　　上面两个函数作用是对于给定的数据集选出最佳的单层决策树.

4.完整的AdaBoost的算法实现 返回目录
　　下面给出完整的AdaBoost的算法实现





def adaBoostTrainDS( dataArr, classLabels, numIt = 40 ):
'''
基于单层决策树的AdaBoost训练过程   
'''
weakClfArr = []
m = np.shape( dataArr )[ 0 ]
D = np.mat( np.ones( ( m, 1 ) ) / m )
aggClassEst = np.mat( np.zeros( ( m, 1 ) ) )
for i in range( numIt ):
# 每一次循环 只有样本的权值分布 D 发生变化
bestStump, error, classEst = buildStump( dataArr, classLabels, D )
print " D: ", D.T
# 计算弱分类器的权重
alpha = float( 0.5 * np.log( ( 1 - error ) / max( error, 1e-16 ) ) )
bestStump[ 'alpha' ] = alpha
weakClfArr.append( bestStump )
print "classEst: ", classEst.T
# 更新训练数据集的权值分布
expon = np.multiply( -1 * alpha * np.mat( classLabels ).T, classEst )
D = np.multiply( D, np.exp( expon ) )
D = D / D.sum()
# 记录对每个样本点的类别估计的累积值
aggClassEst += alpha * classEst
print "aggClassEst: ", aggClassEst.T
# 计算分类错误率
aggErrors = np.multiply( np.sign(aggClassEst) !=
np.mat( classLabels ).T, np.ones( ( m, 1 ) ) )
errorRate = aggErrors.sum() / m
print "total error: ", errorRate, "\n"
# 如果完全正确，终止迭代
if errorRate == 0.0:
break
return weakClfArr
if __name__ == '__main__':
print __doc__
datMat, classLabels = loadSimpData()
#    plt.scatter(datMat[:, 0], datMat[:, 1], c=classLabels, markers=classLabels, s=200, cmap=plt.cm.Paired)
print adaBoostTrainDS( datMat, classLabels, 9 )
AdaBoost　　


　　运行结果
　　



D:  [[ 0.2  0.2  0.2  0.2  0.2]]
classEst:  [[-1.  1. -1. -1.  1.]]
aggClassEst:  [[-0.69314718  0.69314718 -0.69314718 -0.69314718  0.69314718]]
total error:  0.2
D:  [[ 0.5    0.125  0.125  0.125  0.125]]
classEst:  [[ 1.  1. -1. -1. -1.]]
aggClassEst:  [[ 0.27980789  1.66610226 -1.66610226 -1.66610226 -0.27980789]]
total error:  0.2
D:  [[ 0.28571429  0.07142857  0.07142857  0.07142857  0.5       ]]
classEst:  [[ 1.  1.  1.  1.  1.]]
aggClassEst:  [[ 1.17568763  2.56198199 -0.77022252 -0.77022252  0.61607184]]
total error:  0.0
[{'dim': 0, 'ineq': 'lt', 'thresh': 1.3, 'alpha': 0.6931471805599453}, {'dim': 1, 'ineq': 'lt', 'thresh': 1.0, 'alpha': 0.9729550745276565}, {'dim': 0, 'ineq': 'lt', 'thresh': 0.90000000000000002, 'alpha': 0.8958797346140273}]
　　
　　
　　可以看到错误率逐步被降到 $0.0$, 最终的分类器包含 $3$ 个基本分类器.
　　下面基于AdaBoost进行分类，需要做的就只是将弱分类器的训练过程从程序中抽取出来，然后应用到某个具体实例上去。每个弱分类器的结果以其对应的 alpha 值作为权值. 所有这些弱分类器的结果加权求和就得到了最后的结果.
　　AdaBoost分类函数


adaClassify
　　
　　测试



if __name__ == '__main__':
print __doc__
datMat, classLabels = loadSimpData()
#    plt.scatter(datMat[:, 0], datMat[:, 1], c=classLabels, markers=classLabels, s=200, cmap=plt.cm.Paired)
classifierArr = adaBoostTrainDS( datMat, classLabels, 9 )
print adaClassify( [ 0, 0 ], classifierArr )
　　
　　测试结果



[[-0.69314718]]
[[-1.66610226]]
[[-2.56198199]]
[[-1.]]
　　
　　可以发现，随着迭代进行，数据点 $[0, 0]$ 的分类确信度越来越强.
　　5.总结 返回目录
　　AdaBoost的优点：泛化错误率低，可以用在大部分分类器上，无参数调整（自适应）.
　　缺点：对离群点敏感.