|
|
1. 前言
前面博客介绍了CTR预估中的贝叶斯平滑方法的原理http://www.cnblogs.com/bentuwuying/p/6389222.html。
这篇博客主要是介绍如何对贝叶斯平滑的参数进行估计,以及具体的代码实现。
首先,我们回顾一下前文中介绍的似然函数,也就是我们需要进行最大化的目标函数:
下面我们就基于这个目标函数介绍怎样估计参数。
2. 参数估计的几种方法
1. 矩估计
矩估计在这里有点乱入的意思:),因为它其实不是用来最大化似然函数的,而是直接进行参数的近似估计。
矩估计的方法要追溯到19世纪的Karl Pearson,是基于一种简单的 “替换” 思想建立起来的一种估计方法。 其基本思想是用样本矩估计总体矩. 由大数定理,如果未知参数和总体的某个(些)矩有关系,我们可以很自然地来构造未知参数的估计。具体计算步骤如下:
1)根据给出的概率密度函数,计算总体的原点矩(如果只有一个参数只要计算一阶原点矩,如果有两个参数要计算一阶和二阶)。由于有参数这里得到的都是带有参数的式子。比如,有两个参数时,需要先计算出:期望
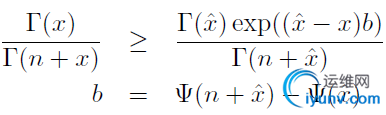 ; 方差
; 方差
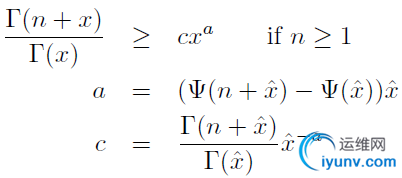 。在Beta分布中,可以计算得到,E(x) = α / (α+β),D(x) = αβ / (α+β)2(α+β+1)。
。在Beta分布中,可以计算得到,E(x) = α / (α+β),D(x) = αβ / (α+β)2(α+β+1)。
2)根据给出的样本,按照计算样本的原点矩。通常它的均值mean用
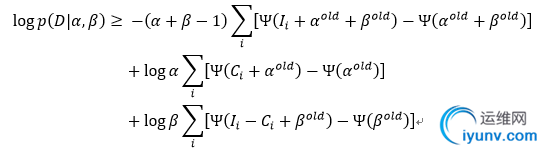 表示,方差var用
表示,方差var用
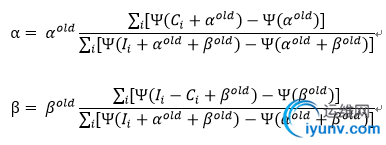 表示。(另外提一句,求时,通常用n-1为底。这样是想让结果跟接近总体的方差,又称为无偏估计)
表示。(另外提一句,求时,通常用n-1为底。这样是想让结果跟接近总体的方差,又称为无偏估计)
3)让总体的原点矩与样本的原点矩相等,解出参数。所得结果即为参数的矩估计值。这里有,mean = E(x) = α / (α+β),var = D(x) = αβ / (α+β)2(α+β+1)。于是乎,我们可以求得α,β:
α = [mean*(1-mean)/var - 1] * mean
β = [mean*(1-mean)/var - 1] * (1-mean)
2. Fixed-point iteration
首先构造出似然函数,然后利用Fixed-point iteration来求得似然函数的最大值。
1)首先给出参数的一个初始值(通常可以使用矩估计得到的结果作为初始值)。
2)在初始值处,构造似然函数的一个紧的下界函数。这个下界函数可以求得其最大值处的闭式解,将此解作为新的估计用于下一次迭代中。
3)不断重复上述(2)的步骤,直至收敛。此时便可到达似然函数的stationary point。如果似然函数是convex的,那么此时就是唯一的最优解。
其实Fixed-point iteration的思想与EM类似。
首先给出两个不等式关系:
1)
2)
由此可以得到对数似然函数的一个下界:
想要得到此下界函数的最大值,可以分别对α,β求偏导,并令之等于零,此时便得到α和β各自的迭代公式:
由此,每次迭代,参数都会达到此次下界函数的最大值处,同时也就使得对应的似然函数值也相应地不断增大,直至收敛到似然函数的最大值处。
3. EM
通过将概率参数作为隐含变量,任何估计概率参数的算法都可以使用EM进一步变成估计个数参数的算法。
(1)E-step:计算出隐含变量p在已观测数据(观测到的每个类别发生的次数,以及每个类别的超参数值的上一轮迭代的取值)下的后验分布,便可以得到完全数据的对数似然函数的期望值。
(2)M-step:对E-step中的期望值求最大值,便可得到相应的超参数的本轮迭代的更新值。
(3)不断重复地运行E-step和M-step,直至收敛。
回来我们这里的问题上,在有了观测到的每个类别发生的次数,以及每个类别的超参数值的上一轮迭代的取值后,隐含变量p的后验分布为:
而此时的完全数据的对数似然函数的期望为:
其中,
于是乎,我们可以对完全数据的对数似然函数的期望求最大值,从而得到α,β的更新值,有很多方法,直接求偏导,梯度下降,牛顿法等。
但是呢,此时我们并不需要非常精确地求得它的最大值,而是仅仅用牛顿法迭代一次。相比于精确地求得最大值,这种方法在每次迭代时只有一半的计算量,但是迭代次数会超过两倍。
牛顿法的迭代可见:
3. 代码实现
#!/usr/bin/python
# coding=utf-8
import numpy
import random
import scipy.special as special
import math
from math import log
class HyperParam(object):
def __init__(self, alpha, beta):
self.alpha = alpha
self.beta = beta
def sample_from_beta(self, alpha, beta, num, imp_upperbound):
sample = numpy.random.beta(alpha, beta, num)
I = []
C = []
for click_ratio in sample:
imp = random.random() * imp_upperbound
#imp = imp_upperbound
click = imp * click_ratio
I.append(imp)
C.append(click)
return I, C
def update_from_data_by_FPI(self, tries, success, iter_num, epsilon):
'''estimate alpha, beta using fixed point iteration'''
for i in range(iter_num):
new_alpha, new_beta = self.__fixed_point_iteration(tries, success, self.alpha, self.beta)
if abs(new_alpha-self.alpha)<epsilon and abs(new_beta-self.beta)<epsilon:
break
self.alpha = new_alpha
self.beta = new_beta
def __fixed_point_iteration(self, tries, success, alpha, beta):
'''fixed point iteration'''
sumfenzialpha = 0.0
sumfenzibeta = 0.0
sumfenmu = 0.0
for i in range(len(tries)):
sumfenzialpha += (special.digamma(success+alpha) - special.digamma(alpha))
sumfenzibeta += (special.digamma(tries-success+beta) - special.digamma(beta))
sumfenmu += (special.digamma(tries+alpha+beta) - special.digamma(alpha+beta))
return alpha*(sumfenzialpha/sumfenmu), beta*(sumfenzibeta/sumfenmu)
def update_from_data_by_moment(self, tries, success):
'''estimate alpha, beta using moment estimation'''
mean, var = self.__compute_moment(tries, success)
#print 'mean and variance: ', mean, var
#self.alpha = mean*(mean*(1-mean)/(var+0.000001)-1)
self.alpha = (mean+0.000001) * ((mean+0.000001) * (1.000001 - mean) / (var+0.000001) - 1)
#self.beta = (1-mean)*(mean*(1-mean)/(var+0.000001)-1)
self.beta = (1.000001 - mean) * ((mean+0.000001) * (1.000001 - mean) / (var+0.000001) - 1)
def __compute_moment(self, tries, success):
'''moment estimation'''
ctr_list = []
var = 0.0
for i in range(len(tries)):
ctr_list.append(float(success)/tries)
mean = sum(ctr_list)/len(ctr_list)
for ctr in ctr_list:
var += pow(ctr-mean, 2)
return mean, var/(len(ctr_list)-1)
def test():
hyper = HyperParam(1, 1)
#--------sample training data--------
I, C = hyper.sample_from_beta(10, 1000, 10000, 1000)
print I, C
#--------estimate parameter using fixed-point iteration--------
hyper.update_from_data_by_FPI(I, C, 1000, 0.00000001)
print hyper.alpha, hyper.beta
#--------estimate parameter using moment estimation--------
hyper.update_from_data_by_moment(I, C)
print hyper.alpha, hyper.beta
4. 参考文献
1. Click-Through Rate Estimation for Rare Events in Online Advertising
2. Estimating a Dirichlet distribution
版权声明:
本文由笨兔勿应所有,发布于http://www.cnblogs.com/bentuwuying。如果转载,请注明出处,在未经作者同意下将本文用于商业用途,将追究其法律责任。 |
|