logistic regression (Python&Matlab实现)

sam_yu

　　本练习以<机器学习实战>为基础, 重现书中代码, 以达到熟悉算法应用为目的
　　(注:matlab的版本转载自http://blog.csdn.net/llp1992/article/details/45114421 , 感谢原作者的辛劳付出)
　　1.梯度上升算法
　　新建一个logRegres.py文件, 在文件中添加如下代码:



from numpy import *
#加载模块 numpy
def loadDataSet():
dataMat = []; labelMat = []
#加路径的话要写作:open('D:\\testSet.txt','r') 缺省为只读
fr = open('testSet.txt')
#readlines()函数一次读取整个文件,并自动将文本分拆成一个行的列表,
#该列表支持python使用for...in...的结构进行处理 (一次只处理一行)   
for line in fr.readlines():
#strip()函数 删除字符串中的首尾空格或制表符等  
#split()函数 按照符号(制表符)进行分割
lineArr = line.strip().split()
#每一行加入第零维 x0 = 1
dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])
labelMat.append(int(lineArr[2]))
return dataMat, labelMat
def sigmoid(inX): #定义sigmoid函数
return 1.0/(1 + exp(-inX))
def gradAscent(dataMatIn, classLabels):
dataMatrix = mat(dataMatIn)             #转换为numpy内置的矩阵格式
labelMat = mat(classLabels).transpose() #transpose()是转置的作用
m,n = shape(dataMatrix)  #获取矩阵的维数
alpha = 0.001  #设定步长
maxCycles = 500 #设定循环次数
weights = ones((n,1)) #初始化权值
for k in range(maxCycles):              #heavy on matrix operations
h = sigmoid(dataMatrix*weights)     #logistic regression的hypothesis
error = (labelMat - h)              
weights = weights + alpha * dataMatrix.transpose()* error #更新权值
return weights

　　在终端中输入下面的命令:



>>> import logRegres
>>> dataArr,labelMat = logRegres.loadDataSet()
>>> weights = logRegres.gradAscent(dataArr, labelMat) #原书中漏掉了weights =
　　会得到下面的结果, 这个是迭代500次后的结果:
　　matrix([[4.12414349],
　　[0.48007329],
　　[-0.6168482]])
　　得到权重后,就可以把图画下来直观的感受下效果了:
　　在文本中添加如下的代码:



def plotBestFit(weights):
import matplotlib.pyplot as plt #把pyplot重命名为plt, 方便以后使用
dataMat,labelMat=loadDataSet()
dataArr = array(dataMat)
n = shape(dataArr)[0]
xcord1 = []; ycord1 = []
xcord2 = []; ycord2 = []
for i in range(n):
if int(labelMat)== 1: #标签是1的数据
xcord1.append(dataArr[i,1]); ycord1.append(dataArr[i,2]) #第一维和第二维分别放入xcorde1和ycorde1这两个list中
else: #标签是0的数据
xcord2.append(dataArr[i,1]); ycord2.append(dataArr[i,2]) #第一维和第二维分别放入xcorde2和ycorde2这两个list中
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(xcord1, ycord1, s=30, c='red', marker='s') #标签为1的数据标为红色
ax.scatter(xcord2, ycord2, s=30, c='green')           #标签为0的数据标为绿色
x = arange(-3.0, 3.0, 0.1) #其实这里的x = x1, y = x2; 而x0 = 1
y = (-weights[0]-weights[1]*x)/weights[2] # 0 = weight[0]*x0 + weight[1]*x1 + weight[2]*x2 把分离超平面在二维画出来
    ax.plot(x, y)
plt.xlabel('X1'); plt.ylabel('X2');
plt.show()
　　生成如下图示的图片:

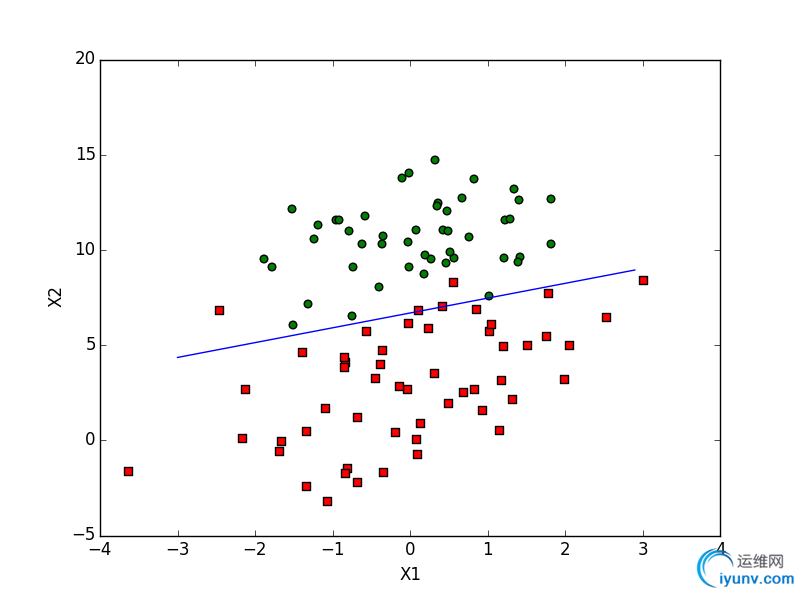
　　下面是matlab版本的实现代码:



function returnVals = sigmoid(inX)
returnVals = 1.0 ./ (1.0 + exp(-inX));
end
　　上面这个是sigmoid函数, 下面的代码会用到



function weight = gradAscend
%%
clc
close all
clear
%%
data = load('testSet.txt');
[row, col] = size(data); %获取数据的行和列
dataMat = data(:, 1:col-1); %去除data的最后一列
dataMat = [ones(row,1) dataMat];%用列1代替
labelMat = data(:, col); %data矩阵的最后一列作为label矩阵
alpha = 0.001; %步进
maxCycle = 500; %设置最大循环次数
weight = ones(col, 1); %初始化权值值
for i = 1:maxCycle
h = sigmoid(dataMat * weight); %logistic回归的hypothesis
error = labelMat - h;
weight = weight + alpha * dataMat' * error;
end
figure
scatter(dataMat(find(labelMat(:) == 0), 2), dataMat(find(labelMat(:) == 0), 3), 3);
hold on
scatter(dataMat(find(labelMat(:) == 1), 2), dataMat(find(labelMat(:) == 1), 3), 5);
hold on
x = -3:0.1:3;
y = (-weight(1)-weight(2)*x)/weight(3);
plot(x.y)
hold off
end
　　效果如下:

　　
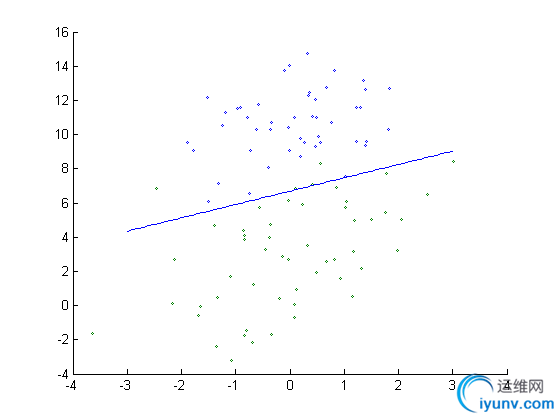
　　2. 随机梯度上升
　　梯度上升算法在每次更新回归系数时需要遍历这个数据集, 倘若数据集规模较大时, 时间空间的复杂度就难以承受了, 一种新的办法是每次只用一个样本点更新回归系数, 这种方法称为随机梯度上升.
　　在原文本中插入一下代码:



def stocGradAscent0(dataMatrix, classLabels):
m,n = shape(dataMatrix)
alpha = 0.01 #设定步进值为0.1
weights = ones(n)   #初始化权值
for i in range(m): #每次只选取一个点进行权值的更新运算可节省不少时间
h = sigmoid(sum(dataMatrix*weights))
error = classLabels - h
weights = weights + alpha * error * dataMatrix
return weights
　　在python命令行窗口输入下述命令:



>>> reload(logRegres)
>>> dataArr,labelMat=logRegres.loadDataSet()
>>> weights=logRegres.stocGradAscent0(array(dataArr),labelMat)
>>> logRegres.plotBestFit(weights)
　　得到如下的图形:

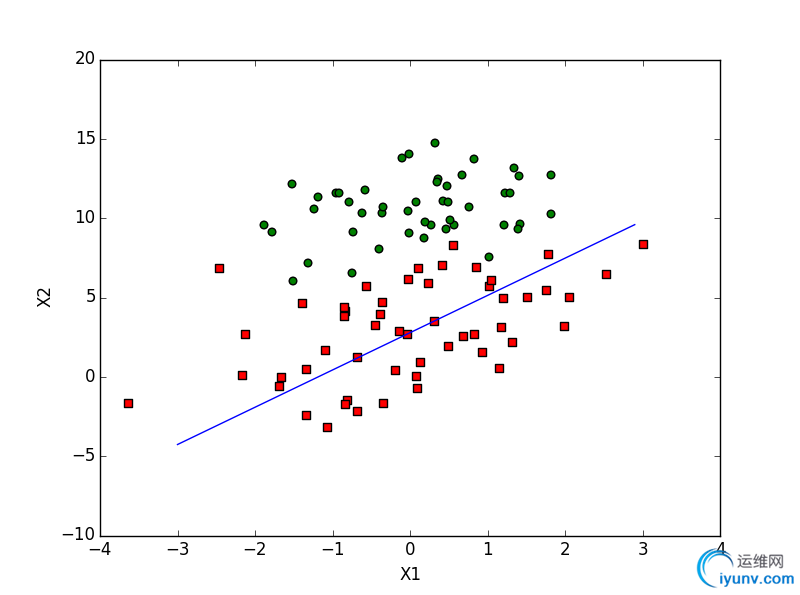
　　matlab版本的代码如下:



function stocGradAscent
%%
%
% Description : LogisticRegression using stocGradAsscent
% Author : Liulongpo
% Time：2015-4-18 10:57:25
%
%%
clc
clear
close all
%%
data = load('testSet.txt');
[row , col] = size(data);
dataMat = [ones(row,1) data(:,1:col-1)];
alpha = 0.01;
labelMat = data(:,col);
weight = ones(col,1);
for i = 1:row
h = sigmoid(dataMat(i,:)*weight);
error = labelMat(i) - h;
weight = weight + alpha * error * dataMat(i,:)'
end
figure
scatter(dataMat(find(labelMat(:)==0),2),dataMat(find(labelMat(:)==0),3),5);
hold on
scatter(dataMat(find(labelMat(:) == 1),2),dataMat(find(labelMat(:) == 1),3),5);
hold on
x = -3:0.1:3;
y = -(weight(1)+weight(2)*x)/weight(3);
plot(x,y)
hold off

end
　　效果图如下所示:

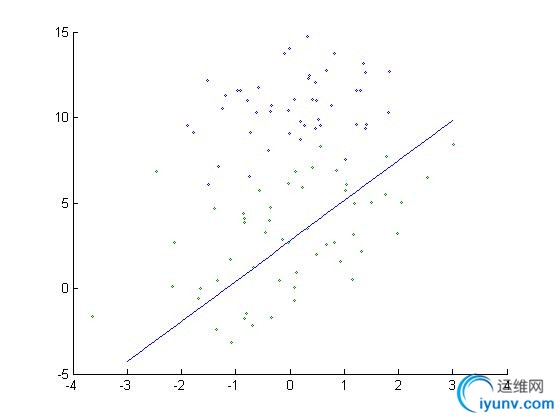
　　似乎效果不太好, 因为训练的次数比较少, 只一轮, 下面修改代码, 并改进其它的一些问题:



def stocGradAscent1(dataMatrix, classLabels, numIter=150): #可自己设定更新的轮数,默认为150
m,n = shape(dataMatrix)
weights = ones(n)   #初始化权值
for j in range(numIter): #第j轮
dataIndex = range(m)
for i in range(m): #第j轮中的第i个数据
alpha = 4/(1.0+j+i)+0.0001    #alpha会随着更新的次数增加而越来越小
randIndex = int(random.uniform(0,len(dataIndex)))#每次的i循环的randIndex的值都不同
h = sigmoid(sum(dataMatrix[randIndex]*weights))
error = classLabels[randIndex] - h
weights = weights + alpha * error * dataMatrix[randIndex]
del(dataIndex[randIndex])
return weights
　　一个重要的改进是alpha 的值不再是一个固定的值, 而是会随着更新的次数增加而越来越小, 但0.0001是它的下限.
　　还有一个改进是 每轮的更新不会按照既有的顺序, 这样可以避免权值周期性的波动.
　　下面是150轮后的图形:

　　
　　
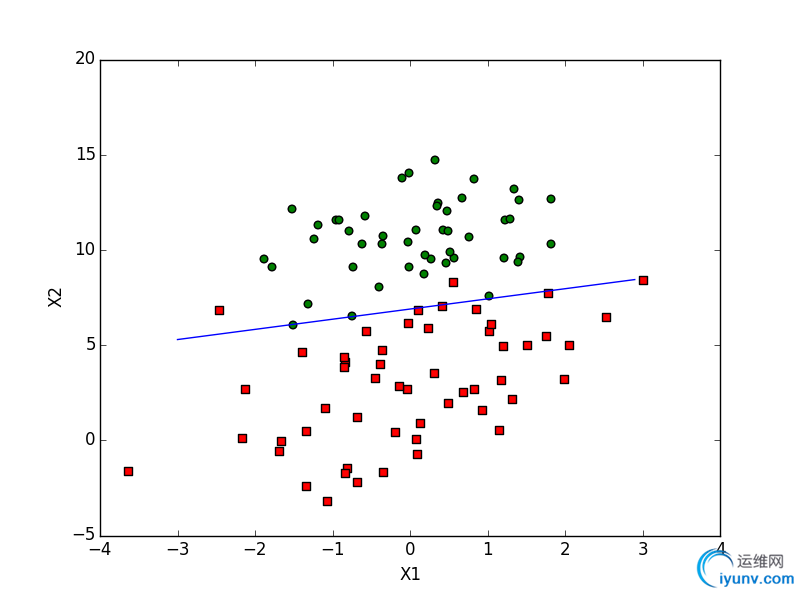
　　可以看到, 随机梯度上升算法比梯度上升算法收敛的更快.
　　下面是matlab的版本:



function ImproveStocGradAscent
%%
clc
clear
close all
%%
data = load('testSet.txt');
[row , col] = size(data);
dataMat = [ones(row,1) data(:,1:col-1)];
numIter = 150;
labelMat = data(:,col);
weight = ones(col,1);
for j = 1: numIter
for i = 1:row
alpha = 4/(1.0+j+i) + 0.0001;
randIndex = randi(row); %产生1到100间的随机数
h = sigmoid(dataMat(randIndex,:)*weight);
error = labelMat(randIndex) - h;
weight = weight + alpha * error * dataMat(randIndex,:)';
end
end
figure
scatter(dataMat(find(labelMat(:)==0),2),dataMat(find(labelMat(:)==0),3),5);
hold on
scatter(dataMat(find(labelMat(:) == 1),2),dataMat(find(labelMat(:) == 1),3),5);
hold on
x = -3:0.1:3;
y = -(weight(1)+weight(2)*x)/weight(3);
plot(x,y)
hold off
end
　　效果如下:

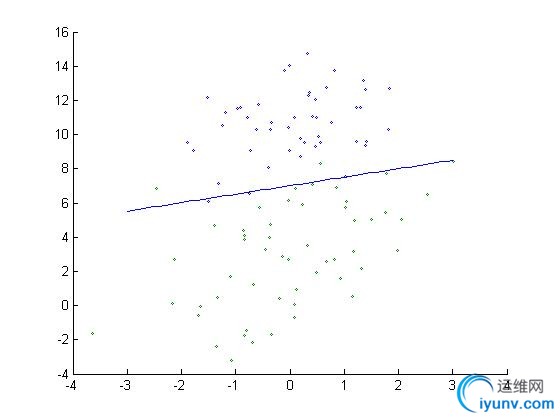
　　3. 一个实际的例子: 预测病马是否能够存活
　　这里每个病马有21个特征:



def classifyVector(inX, weights): #预测函数
prob = sigmoid(sum(inX*weights))
if prob > 0.5: return 1.0
else: return 0.0
def colicTest():
frTrain = open('horseColicTraining.txt'); frTest = open('horseColicTest.txt')
trainingSet = []; trainingLabels = []
for line in frTrain.readlines(): #训练集有299行
currLine = line.strip().split('\t') #每一行的currLine有22个元素
lineArr =[]
for i in range(21): #把currLine的前21个元素放入一个list中去
            lineArr.append(float(currLine))
trainingSet.append(lineArr) # 再把这个list放入一个更大的list中去
trainingLabels.append(float(currLine[21])) #数据集的最后一列是标签列
   
trainWeights = stocGradAscent1(array(trainingSet), trainingLabels, 1000) #训练1000轮
   
errorCount = 0; numTestVec = 0.0
for line in frTest.readlines(): #测试集有67个数据
numTestVec += 1.0 #从0开始, 每测试一个,数目加1
currLine = line.strip().split('\t')
lineArr =[]
for i in range(21):
lineArr.append(float(currLine)) #生成每个测试数据的list
if int(classifyVector(array(lineArr), trainWeights))!= int(currLine[21]): #如果预测值与真实值不等
errorCount += 1 #则错误加1
errorRate = (float(errorCount)/numTestVec)
print "the error rate of this test is: %f" % errorRate
return errorRate
def multiTest():
numTests = 10; errorSum=0.0
for k in range(numTests): #测试10次, 求平均
errorSum += colicTest()
print "after %d iterations the average error rate is: %f" % (numTests, errorSum/float(numTests))
　　运行结果如下:
　　>>> logRegres.multiTest()
logRegres.py:19: RuntimeWarning: overflow encountered in exp
  return 1.0/(1+exp(-inX))
the error rate of this test is: 0.328358
the error rate of this test is: 0.268657
the error rate of this test is: 0.313433
the error rate of this test is: 0.388060
the error rate of this test is: 0.268657
the error rate of this test is: 0.358209
the error rate of this test is: 0.343284
the error rate of this test is: 0.268657
the error rate of this test is: 0.432836
the error rate of this test is: 0.313433
after 10 iterations the average error rate is: 0.328358