sierpinski triangle 2d in maya(with python API 2.0)

wsxxz

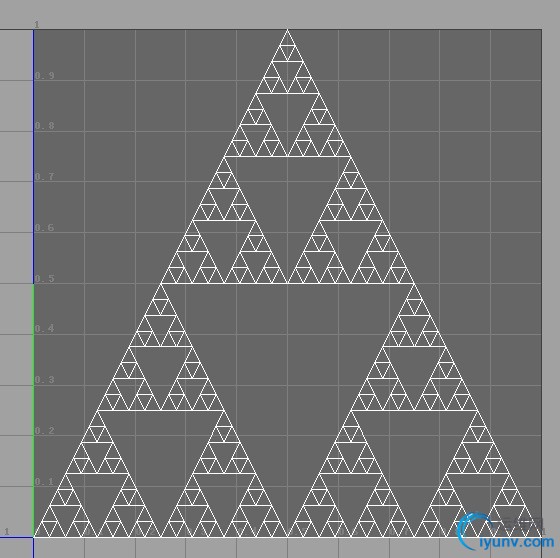
在国庆前我刚好完成手上的工作,有两三天的空闲,于是就去研究了一下分形就当是练习算法,谢尔宾斯基三角形就是其中一个,关于它可以看http://en.wikipedia.org/wiki/Sierpinski_triangle
这里我们使用掏(去)心法和python API 2.0来实现谢尔宾斯基三角形2d(还存在3d的)版本.
算法很简单

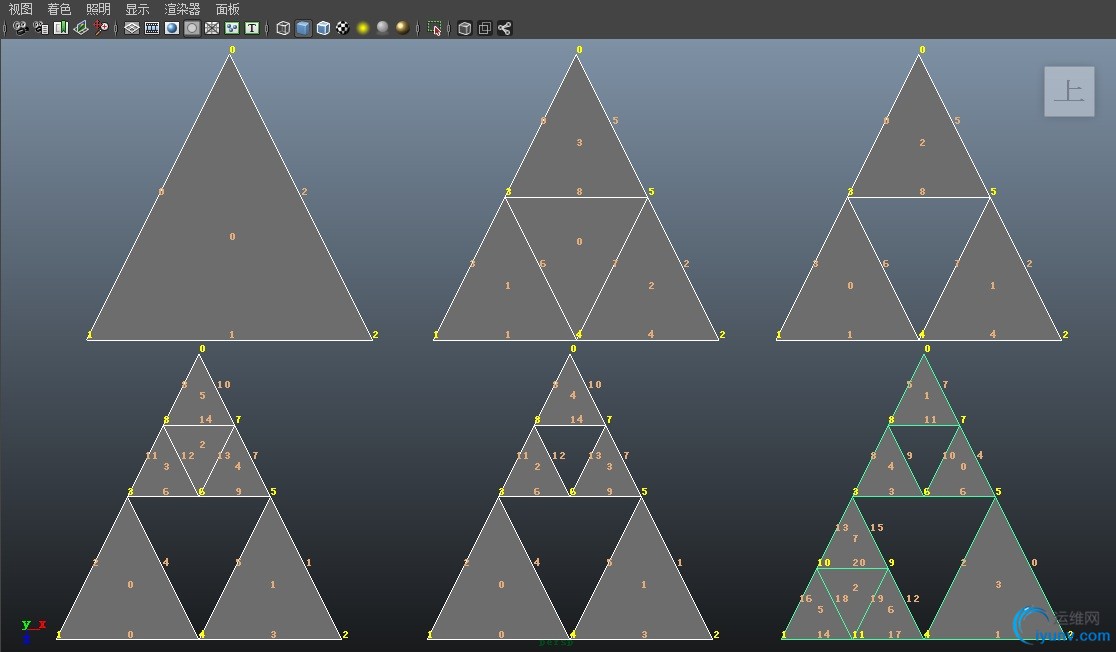
• 创建或得到一个三角形,等腰三角形最好,但不是等腰也行,只不过看起来有点别扭而已
  
• 然后根据每条边的中点进行分割,可以得到4个三角形,把中间的三角形删除
  
• 把剩下的n个三角形重复第二步的分割和删除
  
• 不停的重复第二和第三步
  

import maya.api.OpenMaya as om
from maya import cmds
def sierpinskiTriangle_2d(loop=1):
triPoints = (om.MPoint(0, 0, -10), om.MPoint(-10, 0, 10), om.MPoint(10, 0, 10))
uValue = (0, 0.5, 1)
vValue = (0, 1, 0)
meshFn = om.MFnMesh()
meshFn.create(triPoints, (3,), (0, 1, 2), uValue, vValue)
meshFn.assignUVs((3,), (0, 1, 2))
name = meshFn.name()
for j in range(loop):
for i in range(meshFn.numPolygons):
cmds.select("%s.f[%d]" % (name, i), r=1)
edges = cmds.polyInfo(fe=1)[0].split()[-3:]
meshFn.split(((meshFn.kOnEdge, int(edges[2]), 0.5), (meshFn.kOnEdge, int(edges[1]), 0.5), (meshFn.kOnEdge, int(edges[0]), 0.5), (meshFn.kOnEdge, int(edges[2]), 0.5)))
meshFn.deleteFace(meshFn.numPolygons - 1)
meshFn.updateSurface()
cmds.select(name, r=1)
cmds.hyperShade(a="lambert1")
cmds.select(cl=1)
创建一个三角形
triPoints = (om.MPont(0, 0, -10), om.MPont(10, 0, 10), om.MPont(10, 0, 10))
uValue = (0, 0.5, 1)
vValue = (0, 1, 0)
meshFn = om.MFnMesh()
meshFn.create(triPoints, (3,), (0, 1, 2), uValue, vValue)
meshFn.assignUVs((3,), (0, 1, 2))
使用
om.MFnMesh.create()
来创建多边形,你需要提供多边形的所有顶点坐标,就是一个om.MPoint()或om.MFloatPoint()的列表我们的三角形只有3个顶点.
triPoints = (om.MPont(0, 0, -10), om.MPont(10, 0, 10), om.MPont(10, 0, 10))
然后是每个面有多少个顶点数;
接着是每个面应该由哪些顶点而构成;
uv信息是可以不提供的,不提供的话创建出来的多边形就是没uv的,uValue是一个基于uvId(uv顶点)排列的uv坐标数组,vValue也一样.我们只有3个uv顶点,我希望它们的坐标是(0, 0), (0.5, 1), (1, 0).
还有一个parent参数,也是一个可选参数,如果你提供了,那创建出来的多边形就会以你提供的节点来做父节点,不提供则创建一个transform节点来做父节点.我们这里不需要,所以忽略.
所有信息都提供了就可以创建多边形了
meshFn = om.MFnMesh()
meshFn.create(triPoints, (3,), (0, 1, 2), uValue, vValue)
三角形是创建了,但你会发现它是没有uv的,我们明明就提供了uv信息;其实是这样的om.MFnMesh.create()只是把你传递的uv信息保存而已,并不会真正的去创建uv map,为了让我们传递的uv信息被运用到模型上我们需要调用
meshFn.assignUVs((3,), (0, 1, 2))
第一个参数,uvCounts,是一个列表,每个uv面的uv顶点的数量;
uvIds,也是一个列表,是每个uv面的对应的uvId.
我们的三角形只有一个面,3个顶点,所以是(3,), (0, 1, 2)
到这里就进入算法的后面3步了
for j in range(loop):
是算法中的第四步,不停的重复第二,第三步;
for i in range(meshFn.numPolygons):
cmds.select("%.f[%d]" % (name, i), r=1)
edges = cmds.polyInfo(fe=1)[0].split()[-3:]
meshFn.split(((meshFn.kOnEdge, int(edges[2]), 0.5), (meshFn.kOnEdge, int(edges[1]), 0.5), (meshFn.kOnEdge, int(edges[0]), 0.5), (meshFn.kOnEdge, int(edges[2]), 0.5)))
meshFn.deleteFace(meshFn.numPolygons - 1)
meshFn.updateSurface()
就是对每个三角形进行分割并删除中间的三角形.
在python API 2.0多边形的顶点数,面数,uv数,边数等等都变成了,MFnMesh的实例属性而不是1.0中的方法,这更符合oop的概念,用起来也更简单方便,运行速度也相对快.
meshFn.numPolygons
# API 1.0
meshFn.numPolygons()
需要注意的是不要以为它们是实例属性就随便更改它们的数值,实际上它们是只读属性,就是你只能读取它们的值,不能覆盖或修改,如果你尝试修改,将会引发错误.
为了能将三角形进行分割,我们先要得到当前三角形的3条边,为了简单我就直接使用cmds
cmds.select("%.f[%d]" % (name, i), r=1)
edges = cmds.polyInfo(fe=1)[0].split()[-3:]
om.MFnMesh.split()有两中分割方式,一种是利用边上的点进行分割,就是提供两条边以上,每条边拿出一点来进行分割,另一种是拿面里面的点来进行分割,这个点不能是在所有边上面,也不能是面之外的点.也可以同时使用这两中方法.
这里我们需要在边的中点进行分割,所以先用om.MFnMesh.kOnEdge来确保在边上进行分割,然后指定是哪条边(的id)也就是上面得到的边,因为返回的是字符串列表,所以需要转换成int,最后是你希望在边上的点的位置,这个位置是基于百分比来计算的,所以我们需要0.5
meshFn.split(((meshFn.kOnEdge, int(edges[2]), 0.5), (meshFn.kOnEdge, int(edges[1]), 0.5), (meshFn.kOnEdge, int(edges[0]), 0.5), (meshFn.kOnEdge, int(edges[2]), 0.5)))
分割完成后我们需要把中间的三角形删除
meshFn.deleteFace(meshFn.numPolygons - 1)
为了能在下一个循环中得到正确的多边形信息,我们需要对多边形进行更新,实际上是只要你对多边形进行了添加或是删除的动作都应该调用下面的方法
meshFn.updateSurface()
最后我们创建的多边形是没有赋予材质的,给它一个材质
cmds.select(name, r=1)
cmds.hyperShade(a="lambert1")
cmds.select(cl=1)
如果你有兴趣的话,可以使用cmds来实现这个算法,或是pymel,又或是python API 1.0,除了pymel我都实现过了,最让我恶心的是API 1.0.
谢尔宾斯基三角形还有3d的版本,也以尝试去实现,挺好玩的.