第六章 支持向量机

yao000

第六章 支持向量机
　　Support Vector Machines（SVM）——支持向量机。SVM最流行的一种实现-序列最小优化（Sequential Minimal Optimization，SMO）
　　支持向量——离分隔超平面最近的那些点。
　　超平面可以表示成：
　　\[ f(x)=w^T x + b  \]
　　其中：\( w = \sum\limits_{i = 1}^n {\alpha _i} {y _i} {\left\langle {x _i,x} \right\rangle} \)
　　
然后分类函数可以转化为：
　　\[ f(x) = \sum\limits_{i = 1}^n {\alpha _i} {y _i} {\left\langle {x _i,x} \right\rangle} + b \]

　　上图中，中间的实线就是寻找的最优超平面，其到两条虚线边界的距离相等，这个距离就是几何距离：\(\frac{y _i (w^T {x _i} + b)}{\left\| w \right\|}\)，两条虚线间隔边界之间的距离等于2倍的几何距离，而虚线间隔边界上得点就是支持向量。由于在写支持向量刚好在虚线间隔边界上，所以它们满足\( y (w^T x + b) = 1\)，对于所有不是支持向量的点，显然有\( y (w^T x + b) > 1\)。

1.简化SMO算法（只是贴了代码——详细介绍在完整版SMO算法里面）
　　

def loadDataSet(fileName): #导入数据　　dataMat = []; labelMat = []
　　fr = open(fileName)
　　for line in fr.readlines():
　　lineArr = line.strip().split('\t')
　　dataMat.append([float(lineArr[0]), float(lineArr[1])])
　　labelMat.append(float(lineArr[2]))
　　return dataMat,labelMat
　　

　　
def selectJrand(i,m): #随机选择（函数值不等于输入值，i!=j）
　　j=i #we want to select any J not equal to i
　　while (j==i):
　　j = int(random.uniform(0,m))
　　return j
　　

　　
def clipAlpha(aj,H,L): #用于调整大于H或者小于L的alpha值
　　if aj > H:
　　aj = H
　　if L > aj:
　　aj = L
　　return aj
　　

　　

　　
def smoSimple(dataMatIn,>　　dataMatrix = mat(dataMatIn); labelMat = mat(classLabels).transpose()
　　b = 0; m,n = shape(dataMatrix)
　　alphas = mat(zeros((m,1)))
　　iter = 0
　　while (iter < maxIter):
　　alphaPairsChanged = 0
　　for i in range(m):
　　fXi = float(multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[i,:].T)) + b
　　Ei = fXi - float(labelMat)#if checks if an example violates KKT conditions
　　if ((labelMat*Ei < -toler) and (alphas < C)) or ((labelMat*Ei > toler) and (alphas > 0)):
　　j = selectJrand(i,m)
　　fXj = float(multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[j,:].T)) + b
　　Ej = fXj - float(labelMat[j])
　　alphaIold = alphas.copy(); alphaJold = alphas[j].copy();
　　if (labelMat != labelMat[j]):
　　L = max(0, alphas[j] - alphas)
　　H = min(C, C + alphas[j] - alphas)
　　else:
　　L = max(0, alphas[j] + alphas - C)
　　H = min(C, alphas[j] + alphas)
　　if L==H: print &quot;L==H&quot;; continue
　　eta = 2.0 * dataMatrix[i,:]*dataMatrix[j,:].T - dataMatrix[i,:]*dataMatrix[i,:].T - dataMatrix[j,:]*dataMatrix[j,:].T
　　if eta >= 0: print &quot;eta>=0&quot;; continue
　　alphas[j] -= labelMat[j]*(Ei - Ej)/eta
　　alphas[j] = clipAlpha(alphas[j],H,L)
　　if (abs(alphas[j] - alphaJold) < 0.00001): print &quot;j not moving enough&quot;; continue
　　alphas += labelMat[j]*labelMat*(alphaJold - alphas[j])#update i by the same amount as j
　　#the update is in the oppostie direction
　　b1 = b - Ei- labelMat*(alphas-alphaIold)*dataMatrix[i,:]*dataMatrix[i,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[i,:]*dataMatrix[j,:].T
　　b2 = b - Ej- labelMat*(alphas-alphaIold)*dataMatrix[i,:]*dataMatrix[j,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[j,:]*dataMatrix[j,:].T
　　if (0 < alphas) and (C > alphas): b = b1
　　elif (0 < alphas[j]) and (C > alphas[j]): b = b2
　　else: b = (b1 + b2)/2.0
　　alphaPairsChanged += 1
　　print &quot;iter: %d i:%d, pairs changed %d&quot; % (iter,i,alphaPairsChanged)
　　if (alphaPairsChanged == 0): iter += 1
　　else: iter = 0
　　print &quot;iteration number: %d&quot; % iter
　　return b,alphas
　　

　　运行如下命令：
　　

b, alphas = svmMLiA.smoSimple(dataArr, labelArr, 0.6, 0.001, 40)　　

　　得到：
　　

b=matrix([[-3.83362195]])　　
In [8]:alphas[alphas>0]
　　
Out[8]: matrix([[  1.27443919e-01,   2.41072599e-01,   4.33680869e-18,
　　3.68516518e-01]])
　　

　　为了得到支持向量的个数
　　

In [9]:shape(alphas[alphas>0])　　
Out[9]: (1L, 4L)
　　

　　为了解哪些数据点是支持向量，输入：
　　

for i in range(100):　　if alphas>0.0: print dataArr, labelArr
　　

　　求解w的函数：
　　

def calcWs(alphas,dataArr,classLabels):　　X = mat(dataArr); labelMat = mat(classLabels).transpose()
　　m,n = shape(X)
　　w = zeros((n,1))
　　for i in range(m):
　　w += multiply(alphas*labelMat,X[i,:].T)
　　return w
　　

　　求出的分类超平面为：

2.完整版SMO算法
　　区别： 选择alpha的方式。完整版的Platt SMO算法应用了一些能够提速的启发方法。
　　Platt的文章中定义特征到结果的输出函数为：
　　
\[ u = \vec w \cdot \vec x + b\]
　　
原文是\(-b\)，考虑到之前的\(f(x)=w^T x + b\)，改为\(+b\)。
　　
原始的优化问题为：
　　\[ \begin{array}{l}
\mathop {\max }\limits_{w,b} \frac{1}{\left\| {\vec w } \right\|} \;\;\;\;
s.t.\;{y_i}(\vec w  \cdot {\vec x _i} + b) \ge 1,\forall i
\end{array}\]
　　等价于：
　　\[ \begin{array}{l}
\mathop {\min }\limits_{w,b} \frac{1}{2}{\left\| {\vec w } \right\|^2} \;\;\;\;
s.t.\;{y_i}(\vec w  \cdot {\vec x _i} + b) \ge 1,\forall i
\end{array}\]

2.1 拉格朗日对偶
　　\[ L(w,b,\alpha ) = \frac{1}{2}{\left\| w \right\|^2} - \sum\limits_{i = 1}^n {{\alpha _i}({y_i}({w^T}{x_i} + b) - 1)}  \]
　　令：
　　\[ \theta (w) = \mathop {\max }\limits_{{\alpha _i} \ge 0} L(w,b,\alpha ) \]
　　易知：当约束条件不满足时，例如\({y_i}({w^T}{x_i} + b) < 1\)，显然\(\theta (w) = \infty \)(只要令\(\alpha_i = \infty \))。当所有约束条件都满足时，最优值为\(\theta (w) = \frac{1}{2}{\left\|w\right\|}^2 \)，也就是最初要最小化的量。于是原先的优化问题转换为最小化\(\theta (w)\)。
　　\[ \mathop {\min }\limits_{w,b} \theta (w) = \mathop {\min }\limits_{w,b} \mathop {\max }\limits_{{\alpha _i} \ge 0} L(w,b,\alpha ) = p* \]
　　\[ \mathop {\max }\limits_{{\alpha _i} \ge 0} \mathop {\min }\limits_{w,b} L(w,b,\alpha ) = d* \]
　　其中，\(d* \le p*\)（最小值中的最大值不大于最大值中的最小值），当满足KKT条件时，等号成立。

2.2 对偶问题求解
　　（1）固定\(\alpha\)，让\(L\)关于\(w\)和\(b\)最小化
　　\[ \frac{{\partial L}}{{\partial w}} = 0 \Rightarrow w = \sum\limits_{i = 1}^n {{\alpha _i}{y_i}{x_i}}  \]
　　\[ \frac{{\partial L}}{{\partial b}} = 0 \Rightarrow \sum\limits_{i = 1}^n {{\alpha _i}{y_i} = 0}  \]
　　将以上结果代入\(L\)得到：
　　\[ L(w,b,\alpha ) = \sum\limits_{i = 1}^n {{\alpha _i} - \frac{1}{2}} \sum\limits_{i,j = 1}^n {{\alpha _i}} {\alpha _j}{y_i}{y_j}{x_i}^T{x_j} \]
　　此时，上式只包含\(\alpha\)变量。
　　（2）对\(\alpha\)求极大值
　　此时，目标函数为：
　　\[ \begin{array}{l}
\mathop {\max }\limits_\alpha  W(\alpha ) = \mathop {\max }\limits_\alpha  (\sum\limits_{i = 1}^n {{\alpha _i} - \frac{1}{2}} \sum\limits_{i,j = 1}^n {{\alpha _i}} {\alpha _j}{y_i}{y_j}{x_i}^T{x_j})\\
s.t.\;\;{\alpha _i} \ge 0,\forall i \;\;\& \sum\limits_{i = 1}^n {{\alpha _i}{y_i} = 0}
\end{array} \]
　　这样，便可以求出\(\alpha_i\)（单变量求极值）

2.3 松弛变量处理outliers方法

　　图中黑圈圈起来蓝点是一个outlier（可能是噪声），造成超平面移动，间隔缩小，可见以前的模型对噪声非常敏感。再有甚者，如果离群点在另外一个类中，那么这时候就是线性不可分了。这时候我们应该允许一些点游离并在在模型中违背限制条件（函数间隔大于1）
　　考虑到outlier的问题，约束条件变成了：
　　\[ {y_i}({w^T}{x_i} + b) \ge 1 - {\xi _i},\;\;i = 1,2,...,n \]
　　其中， \(\xi_i \ge 0\)称为松弛变量slack variable，对应数据点 \(x_i\)允许偏离的functional margin的量。因此， \(\xi_i \ge 0\)肯定不能任意大，必须加以限定，新的目标函数变为：
　　\[ \begin{array}{l}
\min \frac{1}{2}{\left\| w \right\|^2} + C\sum\limits_{i = 1}^n {{\xi _i}} \\
s.t.\;\;{y_i}({w^T}{x_i} + b) \ge 1 - {\xi _i},\;{\xi _i} \ge 0,\;\;i = 1,2,...,n
\end{array} \]
　　C用于控制目标函数中两项（“寻找margin最大的超平面”和“保证数据点偏移量最小”）之间的权重。
　　重新构建拉格朗日对偶：
　　\[ L(w,b,\xi ,\alpha ,r) = \frac{1}{2}{\left\| w \right\|^2} + C\sum\limits_{i = 1}^n {{\xi _i} - \sum\limits_{i = 1}^n {{\alpha _i}({y_i}({w^T}{x_i} + b) - 1 + {\xi _i}) - \sum\limits_{i = 1}^n {{r_i}{\xi _i}} } }  \]
　　按照2.2求解对偶问题的方案，得到新的目标函数：
　　\[ \begin{array}{l}
\mathop {\max }\limits_\alpha  W(\alpha ) = \mathop {\max }\limits_\alpha  (\sum\limits_{i = 1}^n {{\alpha _i} - \frac{1}{2}\sum\limits_{i,j = 1}^n {{\alpha _i}{\alpha _j}{y_i}{y_j}\left\langle {{x_i},{x_j}} \right\rangle } } )\\
s.t.\;\;0 \le {\alpha _i} \le C,\;\sum\limits_{i = 1}^n {{\alpha _i}{y_i} = 0,} \;\;i = 1,2,...,n
\end{array} \]
　　此时，与之前的模型唯一不同在于 \(\alpha_i\)多了一个 \(\alpha_i \ge C\)的限制条件。ps：b的求值公式也发生改变，详见2.5 SMO算法。
　　KKT条件
　　\[ \begin{array}{l}
{\alpha _i} = 0\;\;\;\;\;\;\; \Rightarrow \;\;\;{y_i}({w^T}{x_i} + b) \ge 1\\
{\alpha _i} = C\;\;\;\;\;\; \Rightarrow \;\;\;{y_i}({w^T}{x_i} + b) \le 1\\
0 < {\alpha _i} < 0\;\; \Rightarrow \;\;\;{y_i}({w^T}{x_i} + b) = 1
\end{array} \]
　　第一个式子表明在两条间隔线外的样本点前面的系数为0，离群样本点前面的系数为C，而支持向量（也就是在超平面两边的最大间隔线上）的样本点前面系数在(0,C)上。通过KKT条件可知，某些在最大间隔线上的样本点也不是支持向量，相反也可能是离群点。

2.4 核函数
　　当数据线性不可分时，我们可以将特征映射到高维的空间中进行区分。

　　上图，超平面应该是一个圆，而不是一条线，此时超平面的函数可以表示为：
　　\[ {a_1}{X_1} + {a_2}{X_1}^2 + {a_3}{X_2} + {a_4}{X_2}^2 + {a_5}{X_1}{X_2} + {a_6} = 0 \]
　　现在，我们可以构建一个5维的空间，其中5个坐标分别为 \(Z_1=X_1,Z_2=X_1^2,Z_3=X_2,Z_4=X_2^2,Z_5=X_1X_2\)。显然，上面的方程在新的坐标系下可以写成：
　　\[ \sum\limits_{i = 1}^5 {{a_i}{X_i}}  + {a_6} = 0 \]
　　在这个新的5维空间内，我们可以按照之前的线性分类算法来处理。核函数想当于把原来的分类函数：
　　\[ f(x) = \sum\limits_{i = 1}^n {{\alpha _i}{y_i}\left\langle {{x_i},x} \right\rangle }  + b \]
　　映射成：
　　\[ f(x) = \sum\limits_{i = 1}^n {{\alpha _i}{y_i}\left\langle {\phi ({x_i}),\phi (x)} \right\rangle }  + b \]
　　同理， \(\alpha\)可以根据求解如下对偶问题得到：
　　\[ \begin{array}{l}
\mathop {\max }\limits_\alpha  W(\alpha ) = \mathop {\max }\limits_\alpha  (\sum\limits_{i = 1}^n {{\alpha _i} - \frac{1}{2}\sum\limits_{i,j = 1}^n {{\alpha _i}{\alpha _j}{y_i}{y_j}\left\langle {\phi ({x_i}),\phi ({x_j})} \right\rangle } } )\\
s.t.\;\;{\alpha _i} \ge 0,\;\sum\limits_{i = 1}^n {{\alpha _i}{y_i} = 0,} \;\;i = 1,2,...,n
\end{array} \]
　　But，2维映射得到5维，如果是3维将得到19维的新空间——维度爆炸，难以计算。kernel就是解决这个问题的。
　　kernel直接在原来低的维度空间内进行计算，不需要显式的写出映射后的结果。
　　定义核函数为：
　　\[ K(x,z) = \phi {(x)^T}\phi (z) \]
　　（1）假设核函数为：\(K(x,z) = ({(x)^T} z)^2\)
　　展开后，得到：
　　\[ K(x,z) = {({x^T}z)^2} = (\sum\limits_{i = 1}^n {{x_i}{z_i}} )(\sum\limits_{j = 1}^n {{x_j}{z_j}} ) = \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{x_i}} } {x_j}{z_i}{z_j} = \phi {(x)^T}\phi \left( z \right) \]
　　可以通过计算原始特征 \(x\)和 \(z\)內积的平方（时间复杂度O(n)），就等价于计算映射后的特征的內积（O(n^2)）。
　　映射函数（n=2）
　　\[ \phi (x) = \left[ \begin{array}{l}
{x_1}{x_1}\\
{x_1}{x_2}\\
{x_2}{x_1}\\
{x_2}{x_2}
\end{array} \right] \]
　　换句话说，核函数 \(K(x,z) = ({(x)^T} z)^2\)只能在选择上式这样的 \(\phi\)作为映射函数才能等价映射后特征的內积。
　　（2）假设核函数为：\(K(x,z) = ({(x)^T} z +c)^2\)
　　展开后得到：
　　\[ K(x,z) = {({x^T}z + c)^2} = \sum\limits_{i,j = 1}^n {({x_i}{x_j})({z_i}{z_j}) + \sum\limits_{i = 1}^n {(\sqrt {2c} {x_i})(\sqrt {2c} {z_i})} }  + {c^2} \]
　　对应的映射函数（n=2）为:
　　\[ \phi (x) = {\left[ {{x_1}{x_1}\;\;{x_1}{x_2}\;\;{x_2}{x_1}\;\;{x_2}{x_2}\;\;\sqrt {2c} {x_1}\;\;\sqrt {2c} {x_2}\;\;c} \right]^T} \]
　　(3) 举例来说：设两个向量 \(x=(x_1,x_2)^T\)和\(z=(z_1,z_2)^T\)
　　
我们设计核函数为：
　　\[ K(x,z) = ({(x)^T} z +1)^2 \]
　　对应的映射为：
　　\[ \phi (x) = {\left[ {{x_1}{x_1}\;\;{x_1}{x_2}\;\;{x_2}{x_1}\;\;{x_2}{x_2}\;\;\sqrt 2 {x_1}\;\;\sqrt 2 {x_2}\;\;1} \right]^T} \]
　　映射后的內积为：
　　\[ \left\langle {\phi (x),\phi (z)} \right\rangle  = {x_1}^2{z_1}^2 + 2{x _1}{x _2}{z _1}{z _2} + {x_2}^2{z_2}^2 + 2{x_1}{z_1} + 2{x_2}{z_2} + 1 \]
　　这样的映射也满足情况（其实和标准映射一致）：
　　\[ \phi (x) = {\left[ {{x_1}^2\;\;\sqrt 2 {x_1}{x_2}\;\;{x_2}^2\;\;\sqrt 2 {x_1}\;\;\sqrt 2 {x_2}\;\;1} \right]^T} \]
　　这个映射想当于将2维空间映射到了所需的5维空间\(Z_1=x_1,Z_2=x_1^2,Z_3=x_2,Z_4=x_2^2,Z_5=x_1x_2\)。

2.5 SMO算法
　　主要步骤如下：
　　1.选取一对\(\alpha_i\)和\(\alpha_j\)，选取方法采用启发式方法（后面讲）；
　　
2.固定除了\(\alpha_i\)和\(\alpha_j\)之外的其他参数，确定\(W(\alpha)\)极值条件下的\(\alpha_i\)表示（\(\alpha_j\)由\(\alpha_i\)表示）
　　\[ {\alpha _1}{y_1} + {\alpha _2}{y_2} =  - \sum\limits_{i = 3}^n {{\alpha _i}{y_i}}  = \zeta  \]
　　
其中，\(\zeta\)为已知固定值。
　　当\(y_1\)和\(y_2\)异号时，也就是一个为1，一个为-1时，可以表示为下图：

　　\(\alpha_1\)和\(\alpha_2\)既要在矩形方框内，也要在直线上，因此：
　　\[ L = \max (0,{\alpha _2} - {\alpha _1}),H = \min (C,C + {\alpha _2} - {\alpha _1}) \]
　　同理，当当\(y_1\)和\(y_2\)同号时
　　\[ L = \max (0,{\alpha _2} + {\alpha _1} - C),H = \min (C,{\alpha _2} + {\alpha _1}) \]
　　固定其他值后
　　\[ {\alpha _1} = (\zeta  - {\alpha _2}{y_2})/{y_1} \]
　　目标函数 \(W\)可以表示成：
　　\[ W({\alpha _1},{\alpha _2},...,{\alpha _n}) = W((\zeta  - {\alpha _2}{y_2})/{y_1},{\alpha _2}) = a{\alpha _2}^2 + b{\alpha _2} + c \]
　　可以通过对\(W\)求导得到 \(\alpha_2\)，然而还要保证 \(L \le \alpha_2 \le H\)。
　　现在我们综合一下，我们的目标问题是：
　　\[ \begin{array}{*{20}{l}}
{\mathop {\max }\limits_\alpha  W(\alpha ) = \mathop {\max }\limits_\alpha  (\sum\limits_{i = 1}^n {{\alpha _i} - \frac{1}{2}\sum\limits_{i,j = 1}^n {{\alpha _i}{\alpha _j}{y_i}{y_j}K({x_i},{x_j})} } )}\\
{s.t.\;\;0 \le {\alpha _i} \le C,\;\sum\limits_{i = 1}^n {{\alpha _i}{y_i} = 0,} \;\;i = 1,2,...,n}
\end{array} \]
　　现在我们换一下，目标函数变为：（主要为了和Platt的文章一致-变符号-最大值变最小值），此后输出函数变为:
　　\[ u = \vec w \cdot \vec x - b \]
　　\[ \begin{array}{*{20}{l}}
{\mathop {\min }\limits_\alpha  \Psi (\alpha ) = \mathop {\min }\limits_\alpha  (\frac{1}{2}\sum\limits_{i,j = 1}^n {{\alpha _i}{\alpha _j}{y_i}{y_j}K({x_i},{x_j})}  - \sum\limits_{i = 1}^n {{\alpha _i}} )}\\
{s.t.\;\;0 \le {\alpha _i} \le C,\;\sum\limits_{i = 1}^n {{\alpha _i}{y_i} = 0,} \;\;i = 1,2,...,n}
\end{array} \]
　　上式展开：
　　\[ \Psi  = \frac{1}{2}{K_{11}}{\alpha _1}^2 + \frac{1}{2}{K_{22}}{\alpha _2}^2 + s{K_{12}}{\alpha _1}{\alpha _2} + {y_1}{\alpha _1}{v_1} + {y_2}{\alpha _2}{v_2} - {\alpha _1} - {\alpha _2} + {\Psi _{cons\tan t}} \]
　　其中：
　　\[ \begin{array}{l}
{K_{ij}} = K\left( {{x_i},{x_j}} \right)\\
{v_i} = \sum\limits_{j = 3}^n {{y_j}{\alpha _j}^*{K_{ij}} = {u_i} + {b^*} - {y_1}{\alpha _1}^*{K_{1i}} - {y_2}{\alpha _2}^*{K_{2i}}} \\
s = {y_1}{y_2}
\end{array} \]
　　这里的 \(\alpha_1^\)和 \(\alpha_2^\)代表某次迭代前的原始值，因此是常数，而\(\alpha_1\)和 \(\alpha_2\)是待求变量。
　　\[ {y_1}{\alpha _1}^* + {y_2}{\alpha _2}^* = {y_1}{\alpha _1} + {y_2}{\alpha _2} = \zeta  \]
　　左右同时乘以 \(y_1\)：
　　\[ {\alpha _1}^* + s{\alpha _2}^* = {\alpha _1} + s{\alpha _2} = {y_1}\zeta  = w \]
　　可以用 \(\alpha_1\)表示 \(\alpha_2\)并代入上式得到：
　　\[ \frac{{d\psi }}{{d{\alpha _2}}} =  - s{K_{11}}(w - s{\alpha _2}) + {K_{22}}{\alpha _2} - {K_{12}}{\alpha _2} + s{K_{12}}(w - s{\alpha _2}) - {y_2}{v_1} + s + {y_2}{v_2} - 1 = 0 \]
　　最后得到（懒的敲了，去看Platt的论文或者参考文献）：
　　\[ {\alpha _2}({K_{11}} + {K_{22}} - 2{K_{12}}) = {\alpha _2}^*({K_{11}} + {K_{22}} - 2{K_{12}}) + {y_2}({u_1} - {u_2} + {y_2} - {y_1}) \]
　　令：
　　\[ \eta  = {K_{11}} + {K_{22}} - 2{K_{12}} \]
　　得到：
　　\[ {\alpha _2}^{new} = {\alpha _2} + \frac{{{y_2}({E_1} - {E_2})}}{\eta } \]
　　其中：
　　\[ {E_i} = {u_i} - {y_i} \]
　　\[ {\alpha _1}^{new} = {\alpha _1} + s({\alpha _2} - {\alpha _2}^{new}) \]
　　每一步， \(\alpha\)的迭代都需要满足上下边界条件。
　　b值更新
　　\[ \begin{array}{l}
{b_1} = {E_1} + {y_1}({\alpha _1}^{new} - {\alpha _1})K({x_1},{x_1}) + {y_2}({\alpha _2}^{new,clipped} - {\alpha _2})K({x_1},{x_2}) + b\\
{b_2} = {E_2} + {y_1}({\alpha _1}^{new} - {\alpha _1})K({x_1},{x_2}) + {y_2}({\alpha _2}^{new,clipped} - {\alpha _2})K({x_2},{x_2}) + b
\end{array} \]
　　如果 \(\alpha_1^{new}\)在界内，则 \(b^{new} = b_1\);
　　
如果\(\alpha_2^{new,clipped}\)在界内，则\(b^{new} = b_2\);
　　
如果\(\alpha_1^{new}\)和\(\alpha_2^{new,clipped}\)都在界内，那么\(b_1 = b_2\),则\(b^{new} = b_1 = b_2\);
　　
如果\(\alpha_1^{new}\)和\(\alpha_2^{new,clipped}\)都在界上，都满足，一般取\(b^{new} = (b_1 + b_2)/2\);
　　

def smoP(dataMatIn,>
oS = optStruct(mat(dataMatIn),mat(classLabels).transpose(),C,toler, kTup)
　　
iter = 0
　　
entireSet = True; alphaPairsChanged = 0
　　
while (iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)):
　　alphaPairsChanged = 0
　　if entireSet:   #go over all
　　for i in range(oS.m):        
　　alphaPairsChanged += innerL(i,oS)
　　print &quot;fullSet, iter: %d i:%d, pairs changed %d&quot; % (iter,i,alphaPairsChanged)
　　iter += 1
　　else:#go over non-bound (railed) alphas
　　nonBoundIs = nonzero((oS.alphas.A > 0) * (oS.alphas.A < C))[0]
　　for i in nonBoundIs:
　　alphaPairsChanged += innerL(i,oS)
　　print &quot;non-bound, iter: %d i:%d, pairs changed %d&quot; % (iter,i,alphaPairsChanged)
　　iter += 1
　　if entireSet: entireSet = False #toggle entire set loop
　　elif (alphaPairsChanged == 0): entireSet = True  
　　print &quot;iteration number: %d&quot; % iter
　　
return oS.b,oS.alphas
　　

　　数据结构：
　　

class optStruct:
　　
def __init__(self,dataMatIn,>　　self.X = dataMatIn

　　self.labelMat =>　　self.C = C
　　self.tol = toler
　　self.m = shape(dataMatIn)[0]  #行数（100）
　　self.alphas = mat(zeros((self.m,1)))
　　self.b = 0
　　self.eCache = mat(zeros((self.m,2))) #first column is valid flag
　　self.K = mat(zeros((self.m,self.m)))
　　for i in range(self.m):
　　self.K[:,i] = kernelTrans(self.X, self.X[i,:], kTup)
　　

　　优化例程：
　　

def innerL(i, oS):　　Ei = calcEk(oS, i)
　　if ((oS.labelMat*Ei < -oS.tol) and (oS.alphas < oS.C)) or ((oS.labelMat*Ei > oS.tol) and (oS.alphas > 0)):
　　j,Ej = selectJ(i, oS, Ei) #this has been changed from selectJrand
　　alphaIold = oS.alphas.copy(); alphaJold = oS.alphas[j].copy();
　　if (oS.labelMat != oS.labelMat[j]):
　　L = max(0, oS.alphas[j] - oS.alphas)
　　H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas)
　　else:
　　L = max(0, oS.alphas[j] + oS.alphas - oS.C)
　　H = min(oS.C, oS.alphas[j] + oS.alphas)
　　if L==H: print &quot;L==H&quot;; return 0
　　eta = 2.0 * oS.K[i,j] - oS.K[i,i] - oS.K[j,j] #changed for kernel
　　if eta >= 0: print &quot;eta>=0&quot;; return 0
　　oS.alphas[j] -= oS.labelMat[j]*(Ei - Ej)/eta
　　oS.alphas[j] = clipAlpha(oS.alphas[j],H,L)
　　updateEk(oS, j) #added this for the Ecache
　　if (abs(oS.alphas[j] - alphaJold) < 0.00001): print &quot;j not moving enough&quot;; return 0
　　oS.alphas += oS.labelMat[j]*oS.labelMat*(alphaJold - oS.alphas[j])#update i by the same amount as j
　　updateEk(oS, i) #added this for the Ecache                    #the update is in the oppostie direction
　　b1 = oS.b - Ei- oS.labelMat*(oS.alphas-alphaIold)*oS.K[i,i] - oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.K[i,j]
　　b2 = oS.b - Ej- oS.labelMat*(oS.alphas-alphaIold)*oS.K[i,j]- oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.K[j,j]
　　if (0 < oS.alphas) and (oS.C > oS.alphas): oS.b = b1
　　elif (0 < oS.alphas[j]) and (oS.C > oS.alphas[j]): oS.b = b2
　　else: oS.b = (b1 + b2)/2.0
　　return 1
　　else: return 0
　　

　　求出分类超平面为：
　　

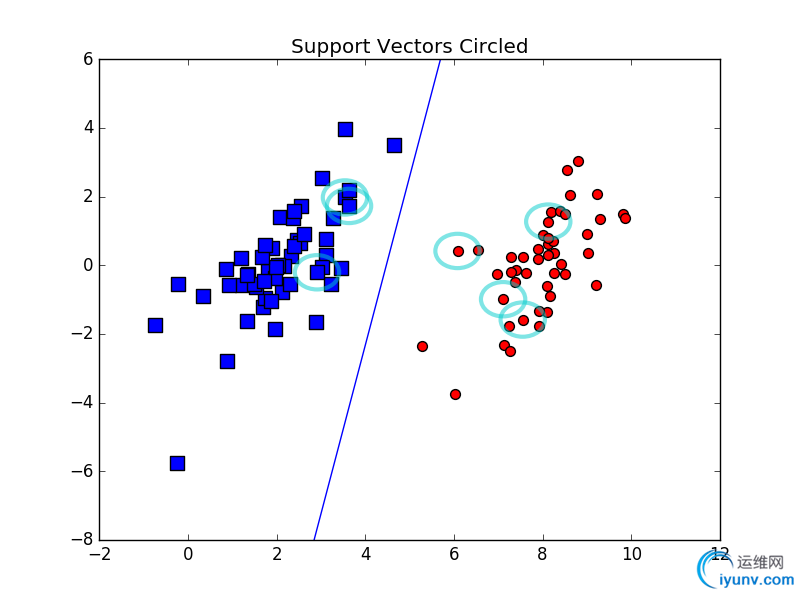
　　由于引入了松弛变量，支持向量会有偏移量。
　　对数据进行分类处理，比如对第一个点进行分类，可以这样输入：
　　

datMat = mat(dataArr)　　
datMat[0]*mat(ws)+b
　　
Out[26]: matrix([[-0.87720838]])
　　

　　如果该值大于0，为1类；如果该值小于0，为-1类。
　　参考文章：
　　1. 支持向量机通俗导论（理解SVM的三层境界）
　　
2. SVM（三），支持向量机，线性不可分和核函数
　　
3. SVM(四） 支撑向量机，二次规划问题