POJ 1860 Currency Exchange（Bellman-Ford）

hcwzwx

　　https://vjudge.net/problem/POJ-1860
　　题意：
　　有多种货币，可以交换，有汇率并且需要支付手续费，判断是否能通过不断交换使本金变多。
　　思路：
　　Bellman-Ford算法。
　　在此之前对贝尔曼-福特算法没怎么了解，当边的权值存在负值的情况下，就可以使用贝尔曼-福特算法。
　　这个算法主要分为三个部分：
　　1、首先初始化，和Dijkstra一样，记录原点到各个点的距离，将原点的值设为0，其余点设为无穷大。
　　2、有n个点的情况下，最多只需要遍历n-1次，每次遍历所有边，进行松弛计算。也就是if（d(v)>d(u)+w(u,v)），d(v)=d(u)+w(u,v)。
　　3、第三部分就是用来检测是否存在复环的，最后再遍历一次所有边，如果存在d(v)>d(u)+w(u,v)，则说明存在负环。
　　
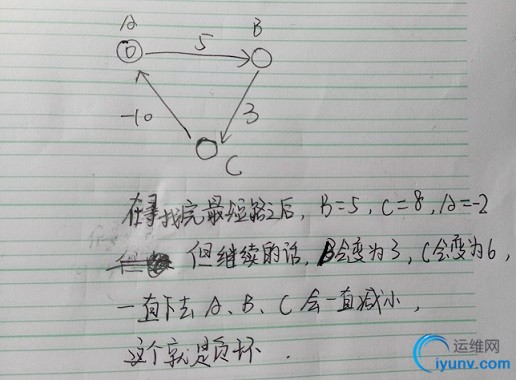
　　回到这道题，这道题目的话就是求一个最大路径，也就是松弛计算的时候计算更大值，最后判断是否存在正环，如果存在，则说明是可以变多的。



1 #include<iostream>
2 #include<algorithm>
3 #include<string>
4 #include<cstring>
5 #include<set>
6 #include<map>
7 using namespace std;
8
9 const int maxn = 200 + 5;
10
11 int n, m, s;   //货币总数、兑换点数量、有第s种货币
12 double v;     //持有的s货币本金
13 int cnt;
14
15 double d[maxn];
16
17 struct node
18 {
19     int a;
20     int b;
21     double rate;
22     double c;
23 }edge[maxn];
24
25 bool bellman_ford()
26 {
27     memset(d, 0, sizeof(d));
28     d = v;
29
30     bool flag;
31     for (int i = 1; i <= n - 1; i++)
32     {
33         flag = false;
34         for (int j = 0; j < cnt; j++)
35         {
36             if (d[edge[j].b] < (d[edge[j].a] - edge[j].c)*edge[j].rate)
37             {
38                 d[edge[j].b] = (d[edge[j].a] - edge[j].c)*edge[j].rate;
39                 flag = true;
40             }
41         }
42         if (!flag)  break;
43     }
44
45     for (int j = 0; j < cnt;j++)
46     if (d[edge[j].b] < (d[edge[j].a] - edge[j].c)*edge[j].rate)
47         return true;
48     return false;
49 }
50
51 int main()
52 {
53     //freopen("D:\\txt.txt", "r", stdin);
54     int a, b;
55     double    rab, cab, rba, cba;
56     while (~scanf("%d%d%d%lf", &n, &m, &s, &v))
57     {
58         cnt = 0;
59         for (int i = 0; i < m; i++)
60         {
61             scanf("%d%d%lf%lf%lf%lf", &a, &b, &rab, &cab, &rba, &cba);
62             edge[cnt].a = a;
63             edge[cnt].b = b;
64             edge[cnt].rate = rab;
65             edge[cnt++].c = cab;
66             edge[cnt].a = b;
67             edge[cnt].b = a;
68             edge[cnt].rate = rba;
69             edge[cnt++].c = cba;
70         }
71         if (bellman_ford())
72             printf("YES\n");
73         else
74             printf("NO\n");
75     }
76     return 0;
77 }