基于 Python Matplotlib 模块的高质量图形输出

vivion32

　　文章来源：
　　http://www.ibm.com/developerworks/cn/linux/l-matplotlib/index.html
　　
　　2005 年  1 月  01 日

Matplotlib 是一个用来绘制二维图形的 Python 模块，它克隆了许多 Matlab 中的函数， 用以帮助 Python 用户轻松获得高质量(达到出版水平)的二维图形。

　　1 关于 Matplotlib 模块
　　Matplotlib
是一个由 John Hunter 等开发的，用以绘制二维图形的 Python 模块。它利用了 Python 下的数值计算模块 Numeric
及 Numarray，克隆了许多 Matlab 中的函数， 用以帮助用户轻松地获得高质量的二维图形。Matplotlib
可以绘制多种形式的图形包括普通的线图，直方图，饼图，散点图以及误差线图等；可以比较方便的定制图形的各种属性比如图线的类型，颜色，粗细，字体的大小
等；它能够很好地支持一部分 TeX 排版命令，可以比较美观地显示图形中的数学公式。Matplotlib 掌握起来也很容易，由于
Matplotlib 使用的大部分函数都与 Matlab 中对应的函数同名，且各种参数的含义，使用方法也一致，这就使得熟悉 Matlab
的用户使用起来感到得心应手。对那些不熟悉的 Matlab 的用户而言，这些函数的意义往往也是一目了然的，因此只要花很少的时间就可以掌握。
　　
Matplotlib 目前包含了37个不同的模块, 如 matlab, mathtext, finance, dates

　　等等，其中与绘图关系最直接的是 matlab 模块。可以用下面的命令装载并查看它提供的函数

>>> import matplotlib.matlab >>> dir(matplotlib.matlab)

　　
　　如果要了解模块中某个函数的使用方法，可以使用 help 命令。如下面的命令

>>> help(legend) >>> help(plot)

　　
　　会返回 legend 和 plot 这两个函数的信息。
　　本文拟通过一些实例来说明 matplotlib 的这些主要特点。相信通过阅读这些例子，您能对 Matplotlib 的使用有一个基本的了解。
　　

回页首

　　

　　2 绘制一组幂函数
　　先从一个简单的例子开始讨论。假设要在一个图形中显示一组幂函数。这组幂函数的基不同，分别为10，自然对数 e 和2。可以用如下 Python 脚本去描绘这组曲线，生成的图形如图1所示。

from matplotlib.matlab import *   x = linspace(-4, 4, 200)   f1 = power(10, x)   f2 = power(e, x)   f3 = power(2, x)     plot(x, f1, 'r',  x, f2, 'b', x, f3, 'g', linewidth=2)   axis([-4, 4, -0.5, 8])   text(1, 7.5, r'$10^x$', fontsize=16)   text(2.2, 7.5, r'$e^x$', fontsize=16)   text(3.2, 7.5, r'$2^x$', fonsize=16)   title('A simple example', fontsize=16)   savefig('power.png', dpi=75)   show()

　　
图1: 一组幂函数

　　程
序的第一行装载了 matlab 模块。接下来的几行语句（至 savefig 之前）好像是在运行 Matlab 程序，因为 linspace，
power, plot，axis, text, title 这些函数在 Matlab 中也存在。这个例子展示了 Matplotlib
中几个比较常用的绘图函数，如 plot，axis，title 等的用法。其中 plot 是一个功能十分强大的函数,
通过改变它的参数选项，可以灵活地修改图形的各种属性，比如选用的线型，颜色，宽度等。
　　

回页首

　　

　　2 显示图形中的数学公式
　　Matplotlib
可以支持一部分 TeX 的排版指令，因此用户在绘制含有数学公式的图形时会感到很方便并且可以得到比较满意的显示效果，所需要的仅仅是一些 TeX
的排版知识。下面的这个例子显示了如何在图形的不同位置上, 如坐标轴标签，图形的标题以及图形中适当的位置处，显示数学公式。相应的 Python
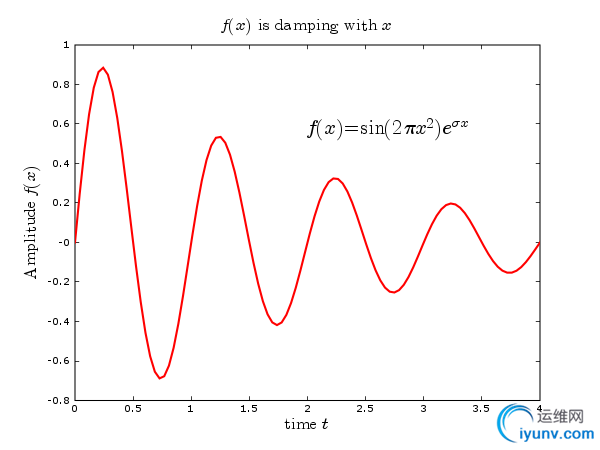
程序如下, 生成的图形见图2。

from matplotlib.matlab import * def  f(x, c):     m1 = sin(2*pi*x)     m2 = exp(-c*x) return multiply(m1, m2) x = linspace(0, 4, 100) sigma = 0.5 plot(x, f(x, sigma), 'r', linewidth=2) xlabel(r'$\rm{time}  \  t$', fontsize=16) ylabel(r'$\rm{Amplitude} \ f(x)$', fontsize=16) title(r'$f(x) \ \rm{is \ damping  \ with} \ x$', fontsize=16) text(2.0, 0.5, r'$f(x) = \rm{sin}(2 \pi  x^2) e^{\sigma x}$', fontsize=20) savefig('latex.png', dpi=75) show()

　　
图2: 图形中数学公式的显示

　　从
程序中可以看出，在 Matplotlib 中进行有关数学公式的排版是很简单的。与 TeX 排版时的约定一样，要插入的公式部分由一对美元符号 $
来进行标识，而具体的排版命令与 TeX
一样。在任何可以显示文本的地方（如轴的标签，标题处等）都可以插入需要的公式。需要注意的是，数学公式所在的字符串开始之处有一个标记
r，表示该字符串是一个 raw string。这是因为排版公式时，字符串所包含的内容必须按照 TeX
的规范，而不是其他的规范，来进行解析。所以使用 raw string
可以避免其它规则解释字符串中某些特殊字符所带来的歧义。从生成的图形可以看到，公式显示的效果是比较美观的。
　　

回页首

　　

　　3 绘制其他格式的图形
　　除
了常用的线图，Matplotlib
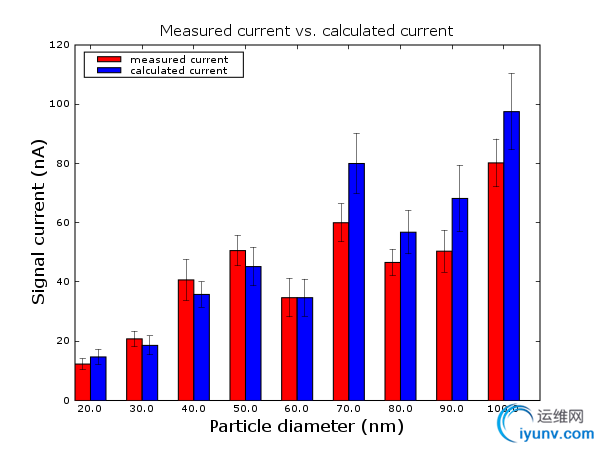
还可以绘制其他种类的图形，如直方图，饼图，误差线图等等。下面是一个处理实验数据的例子。它用直方图的形式比较了实际测量电流和理论计算电流，同时还显
示了测量的误差分布情况。程序首先读取实验数据 current.dat，获得数据后利用函数 bar 进行绘图。

from matplotlib.matlab import  * filename = "d:\\wei\\exp\\current.dat" X = load(filename) dp = X[:, 0] i_mea = X[:, 1] i_mea_err = X[:, 2] i_cal = X[:, 3] i_cal_err = X[:, 4] width = 3 h1 = bar(dp, i_mea, width, color='r', yerr=i_mea_err) h2 = bar(dp+width, i_cal, width, color='b', yerr=i_cal_err) xlabel('Particle diameter (nm)', fontsize=16) xticks(dp+width, dp) ylabel('Signal current (nA)', fontsize=16) title('Measured current vs. calculated current') legend((h1[0], h2[0]), ('measured current', 'calculated current'), loc=2) savefig('current.png', dpi=75) show()

　　
图3 :测量电流 vs. 计算电流

　　从程序中可以看出，函数 load 极大地方便了数据文件的读取工作（不需要自己写代码来处理数据文件了），它的输出直接被传递至函数 bar 中，进而完成直方图和误差线图的绘制。
　　

回页首

　　

　　4 GLP 集合计算结果的可视化
　　Python
是一种比较适合用来进行科学计算的脚本语言，如果利用了 Numeric 及 Numarray 模块，它的计算能力还能得到进一步的增强。
Matplotlib 也充分利用了这两个模块，可以高质量地完成计算结果可视化的工作。下面是一个计算和显示两维好格子点 GLP (Good
Lattice Point Set)集合的例子。 GLP
集合是一种用算法产生的伪随机数的集合,它在一些优化计算中很有用，详细的介绍可以在参考文献里找到。下面的 Python 程序先定义了一个函数
glp(n1, n2) 用以产生需要的 GLP 集合, 接着利用 Matplotlib 来显示它的分布情况（应该是均匀分布的）。

# A two dimensional GLP set # with n1=377,  n2=610 from matplotlib.matlab import * def glp(n1, n2): q = zeros((2, n2), Float) h1 = 1; h2 = n1 for i in arange(n2-1): q[0][ i] = (fmod(h1*(i+1), n2)-0.5)/n2 q[1][ i] = (fmod(h2*(i+1), n2)-0.5)/n2 q[0][n2-1] = (n2-0.5)/n2 q[1][n2-1] = (n2-0.5)/n2 return q n1 = 377; n2 = 610 q = glp(n1, n2) x = q[0, :] y = q[1, :] plot(x, y, 'r.', linewidth=2) axis([0, 1, 0, 1]) title(r'$\rm{GLP \ set \ with} \ n_1 = 377, \ n_2 = 610$') savefig('glp.png', dpi = 75) show()

　　
图4: GLP 集合的分布

　　最
初我们是用 Matlab 来完成这个工作的，现在用 Python 来实现一样很简洁。程序中函数 glp 的实现主要是利用了模快
Numeric，计算得到的结果用 plot 函数直接加以显示，十分方便。这个例子（包括上一个例子）显示了，在利用 Python
进行某些科学及工程计算时，Matplotlib 往往能简洁高效地完成计算结果可视化的工作。
　　

回页首

　　

　　5 工作模式及图形的输出方式
　　最
后简单的介绍一下 Matplotlib 的工作模式以及输出图形的方式。Matplotlib 有两种工作模式：交互模式 (interactive
mode) 以及批处理模式 (batch mode)。很容易理解这两种模式的差别。第一种模式就是在某个 Python Shell
的提示符下逐个运行绘图的命令。
　　第二种模式是先把绘图命令写成一个脚本文件然后在适当的环境中执行这个文件。
最终图形的输出也有两种方式，即 GUI 输出方式和非 GUI 输出方式。简单地说，GUI 方式的输出是把产生的图形直接显示在屏幕上；而非
GUI 方式的输出则是把图形保存为某种格式的文件，比如ps，png格式的文件。不论哪一种方式都与系统使用的 backend 有关
（backend 可以理解为后端的绘图引擎）。与 GUI方式输出有关的 backend 包括 WxPython, TkAgg, Tkinter
等。而与非 GUI 方式有关的 backend 包括 GD, PS，Paint 等。下图总结了目前 Matplotlib
支持的主要backend。
　　
图5: Matplotlib 支持的主要 backend

　　用
户可以根据自己的实际需要选用其中的某种输出方式，当然也可以两种同时使用。以上的几个例子都是同时使用了这两种方式。以上几个 Python
脚本的最后一行命令 show 负责把图形在屏幕上显示出来，而命令 savefig 会把图形保存为相应格式的文件，目前缺省的输出格式是 png
格式。
　　

回页首

　　

　　6 总结
　　作
为一个仍在进行中的项目，Matplotlib 充分利用了 Python 下的 Numeric(Numarray) 模块，提供了一种利用
Python 进行数据可视化的解决方案，进一步加强了 Python 用来进行科学计算的能力。Matplotlib 简单易学，它克隆了众多
Matlab 中的函数，这会让了解 Matlab
的用户受益不少。其他的特点还包括能够绘制多种类型的图形，可以简单灵活对图形的各种属性进行修改，能比较美观地显示图形中的数学公式。与其他的一些绘图
程序相比，如 Gnuplot，Matplotlib 的一个吸引人之处就是输出图形的质量较高。不足之处是 Matplotlib
的功能目前还不是很完善, 比如目前还不能支持三维绘图，对 TeX
排版的支持还不充分等等。不过考虑到它是一个还在进行中的项目，这些就不应求全责备了。总的说来，如果您需要一种可视化的工具，并且希望它能有高质量的输
出效果，那么 Python 的 Matplotlib 模块应该是一个值得考虑的选择。
　　

　　参考资料

• 访问 Matplotlib 的主页
  http://Matplotlib.sourceforge.net 以获得更多关于它的信息
  
• Matplotlib 提供的所有模块可在
  http://Matplotlib.sourceforge.net/classdocs.html 里找到
  
• Gnuplot的主页
  http://www.gnuplot.org
  
• K. T. Fang and Y. Wang, Numer-theoretic Methods in Statistics, 1993, Chapman & Hall
  
• IBM
  developerWorks 网站上由 David Mertz 撰写的一篇很好的关于 Numeric Python 模快的文章:
  Charming Python: Numerical Python -- Working with the numeric and
  numarray packages